Logistic Regression with JMP

What is Logistic Regression?

Logistic regression is a statistical method to predict the probability of an event occurring by fitting the data to a logistic curve using logistic function. The regression analysis used for predicting the outcome of a categorical dependent variable, based on one or more predictor variables. The logistic function used to model the probabilities describes the possible outcome of a single trial as a function of explanatory variables. The dependent variable in a logistic regression can be binary (e.g. 1/0, yes/no, pass/fail), nominal (blue/yellow/green), or ordinal (satisfied/neutral/dissatisfied). The independent variables can be either continuous or discrete.

Logistic Function

Where: z can be any value ranging from negative infinity to positive infinity.
The value of f(z) ranges from 0 to 1, which matches exactly the nature of probability (i.e., 0 ≤ P ≤ 1).
Logistic Regression Equation
Based on the logistic function,

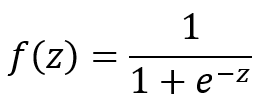
we define f(z) as the probability of an event occurring and z is the weighted sum of the significant predictive variables.

Where: Z represents the weighted sum of all of the predictive variables.

Logistic Regression

Another of way of representing f(z) is by replacing the z with the sum of the predictive variables.

Where: Y is the probability of an event occurring and x’s are the significant predictors.
Notes:

• When building the regression model, we use the actual Y, which is discrete (e.g. binary, nominal, ordinal)
• After completing building the model, the fitted Y calculated using the logistic regression equation is the probability ranging from 0 to 1. To transfer the probability back to the discrete value, we need SMEs’ inputs to select the probability cut point

Logistic Curve

The logistic curve for binary logistic regression with one continuous predictor is illustrated by the following Figure.

Odds

Odds is the probability of an event occurring divided by the probability of the event not occurring.

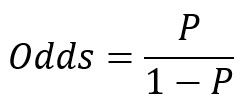
Odds range from 0 to positive infinity.
Probability can be calculated using odds.

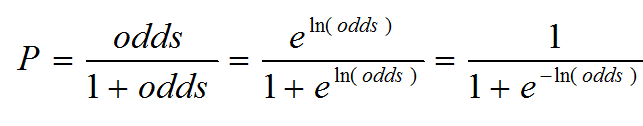
Because probability can be expressed by the odds, and we can express probability through the logistic function, we can equate probability, odds, and ultimately the sum of the independent variables.
Since in logistic regression model

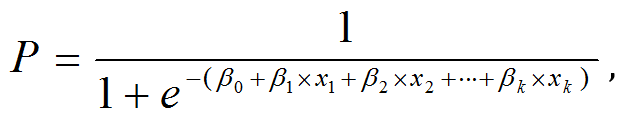
therefore

Three Types of Logistic Regression

• Binary Logistic Regression
  • Binary response variable
  • Example: yes/no, pass/fail, female/male
• Nominal Logistic Regression
  • Nominal response variable
  • Example: set of colors, set of countries
• Ordinal Logistic Regression
  • Ordinal response variable
  • Example: satisfied/neutral/dissatisfied

All three logistic regression models can use multiple continuous or discrete independent variables and can be developed in JMP using the same steps.

How to Run a Logistic Regression in JMP

Case Study: We want to build a logistic regression model using the potential factors to predict the probability that the person measured is female or male.
Data File: “LogisticRegression.jmp”

Response and potential factors:

• Response (Y): Female/Male
• Potential Factors (Xs):
  • Age
  • Weight
  • Oxy
  • Runtime
  • RunPulse
  • RstPulse
  • MaxPulse

Step 1:

1. Click Analyze -> Fit Model
2. Select “Sex” as the Y and all the potential factors into the model effects box
3. Click “Run” button
   

Step 2:

1. The results of the regression model appear automatically
2. Check the p-value of all the independent variables in the model
3. Remove the insignificant independent variable one at a time from the model and rerun the model
4. Repeat step 2.1 until all the independent variables in the model are statistically significantly
            

Since the p-values of all the independent variables are higher than the alpha level (0.05), we need to remove the insignificant independent variables one at a time from the model, starting from the one with the highest p-value. MaxPulse has the highest p-value (0.9390), so it would be removed from the model first.

Step 3: Re-Open Your Last Dialog Box

1. Click the red triangle next to “Nominal Logistic Fit for Sex”
2. Select “Model Dialog”
3. The dialog box used to create your last model opens.
4. Remove the variable MaxPulse
5. Follow these same steps with each successive Logistic Regression output screen until you no longer have to remove variables.
   
   

After removing MaxPulse from the model, the p-values of all the independent variables are still higher than the alpha level (0.05). We need to continue removing the insignificant independent variables one at a time from the model, starting from the one with the highest p-value. RunPulse has the highest p-value (0.4516), so it would be removed from the model next.

After removing RunPulse from the model, the p-values of all the independent variables are still higher than the alpha level (0.05). We need to continue removing the insignificant independent variables one at a time from the model, starting from the one with the highest p-value. RunTime has the highest p-value (0.2684) so it would be removed from the model next.

After removing RunTime from the model, the p-values of all the independent variables are still higher than the alpha level (0.05). We need to continue removing the insignificant independent variables one at a time from the model, starting from the one with the highest p-value. Age has the highest p-value (0.3821), so it would be removed from the model next.

After removing Age from the model, the p-values of all the independent variables are still higher than the alpha level (0.05). We need to continue removing the insignificant independent variables one at a time from the model, starting from the one with the highest p-value. RstPulse has the highest p-value (0.3857), so it would be removed from the model next.

After removing RstPulse from the model, the p-values of all the independent variables are still higher than the alpha level (0.05). We need to continue removing the insignificant independent variables one at a time from the model, starting from the one with the highest p-value. Weight has the highest p-value (0.0755), so it would be removed from the model next.

After removing Weight from the model, the p-value of the only independent variable “Oxy” is lower than the alpha level (0.05). There is no need to remove “Oxy” from the model.

Step 4:

• Analyze the model results and see how the probability change with the change of the independent variable.
• The logistic curve with Y axis indicates the probability of being male and the X axis indicating the value of oxygen uptake.
• When the amount of oxygen uptake increases, the probability of the person measured being male increases accordingly.
• The R-squared is 20.06%. The R-squared of logistic regression is in general lower than the R-squared of the traditional multiple linear regression model.

Step 5:

1. Click on the red triangle button next to “Nominal Logistic Fit for Sex”
2. Click on “Save Probability Formula”
3. The probabilities of the person measured being male and female are added to the right end of the data table.
4. If the probability of a person measured being male is higher than 0.5, it is predicted that the person is male and the prediction is in the last column in the data table.
   

Step 6:

1. Click on the red triangle button next to “Nominal Logistic Fit for Sex”
2. Select “Profiler”
3. The Prediction Profiler appears
   

Model summary: By changing the value of oxygen uptake, the probability of the person being male or female changes accordingly.