Paired T Test

Hypothesis testing allows us to validate an assumption or a “hypothesized” conclusion. We are able to accomplish this by using data and statistical measures that give us a better understanding of the risks we are taking if we reject or fail to reject the null hypothesis. Using a Paired t Test is necessary when the two samples being compared have a dependency. When no dependency exists, a 2-Sample t Test will generally suffice. Therefore, it is important to know that you will need a Paired t Test when your samples have dependency.

It is also accepted practice to test the Normality of the data points. Normality is an assumption for many hypothesis tests including the Paired t Test. Normality should be determined in order to ensure that the Paired t Test is the proper test given your data.

The Null and Alternative hypothesis statements for the Paired t Test are:
Ho = μ1−μ2=0 (Ho is the null hypothesis, it states that the difference between mean1 and mean2 is equal to zero)
Ha = μ1-μ2 is not =0 (Ha is the alternate hypothesis, it states that the difference between mean1 and mean2 is not equal to zero)

An example for a Paired t Test is shown below:
An analyst at the division level of the corporation believes that two factories which are making the exact same product at the same specifications using raw materials from the same supplier are performing differently when they should not be. (IMPORTANT: raw material in this instance is the dependency that dictates we should use a Paired t test. If both factories use the same raw materials, then factory A and factory B are not entirely independent). The Analyst shares her observations with a Six Sigma Black Belt who decides to perform a planned study to collect 30 samples and test the analyst’s hypothesis. Below are the results:

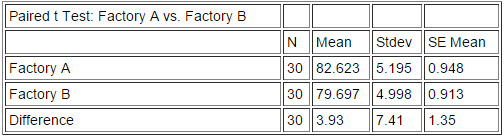
95% Confidence Interval (CI) mean difference: (1.16, 6.69)
T-Test of mean difference = 0 (vs not = 0): T-Value = 2.90
P-Value = 0.007

Interpretation
The confidence interval for the mean difference between the two factories does not include zero, which suggests a difference between them. The small p-value (p = 0.007) further suggests that the data are inconsistent with the Null (Ho), that is, the two factories do not perform equally. More specifically, Factory A (mean = 79.697) performed better than Factory B (mean = 83.623).
Final conclusion for this paired t test; Reject the Null (reject Ho) and conclude there is a statistically significant difference between factory A and Factory B. The analyst was correct.