Box Cox Transformation with SigmaXL

Box Cox Transformation

• Data transforms are usually applied so that the data appear to more closely meet assumptions of a statistical inference model to be applied or to improve the interpret-ability or appearance of graphs.
• Power transformation is a class of transformation functions that raise the response to some power. For example, a square root transformation converts X to X^1/2
• Box Cox transformation is a popular power transformation method developed by George E. P. Box and David Cox.

Use SigmaXL to Perform a Box-Cox Transformation

SigmaXL provides the best Box-Cox transformation with an optimal λ that minimizes the model SSE (sum of squared error). Here is an example of how we transform the non-normally distributed response to normal data using Box-Cox method.
Data File: “Box-Cox” tab in “Sample Data.xlsx”

Step 1: Test the normality of the original data set.

1. Select the entire range of “Y” in column H
2. Click SigmaXL -> Graphical Tool -> Histograms & Descriptive Statistics
3. A new window named “Histograms & Descriptive” pops up and the selected range automatically appears in the box below “Please select your data”.
   
4. Click “Next >>”
5. A new window named “Histograms & Descriptive Statistics” pops up.
6. Select “Y” as “Numeric Data Variables (Y)”
   
7. Click “OK>>”
8. The analysis results are shown automatically in the new spreadsheet “Hist Descript(1)”
   

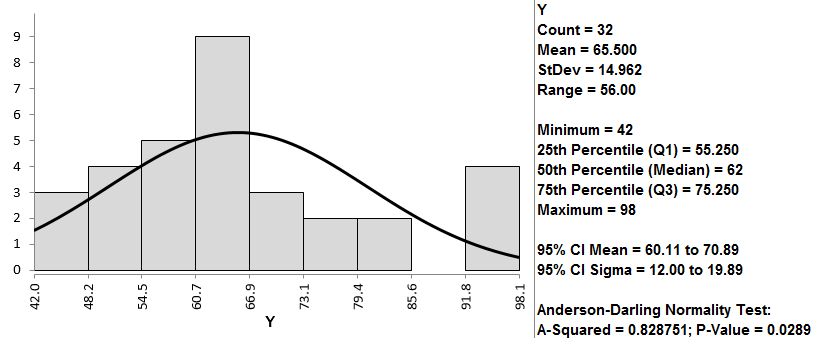
Normality Test:

• H₀: The data are normally distributed.
• H₁: The data are not normally distributed.

If p-value > alpha level (0.05), we fail to reject the null hypothesis. Otherwise, we reject the null. In this example, p-value = 0.029 < alpha level (0.05). The data are not normally distributed.

Step 2: Run the Box-Cox Transformation:

1. Select the entire range of Y in column H
2. Click SigmaXL -> Process Capability -> Nonnormal -> Box-Cox Transformation
3. A new window named “Box-Cox Transformation” pops up and the selected range appears automatically in the box under “Please select your data”
   
4. Click “Next >>”
5. A new window also named “Box-Cox Transformation” pops up.
6. Select “Y” as “Numeric Data Variables (Y)”
   
7. Click “OK>>”
8. The analysis results are shown automatically in the new spreadsheet “Box-Cox (1)”
   

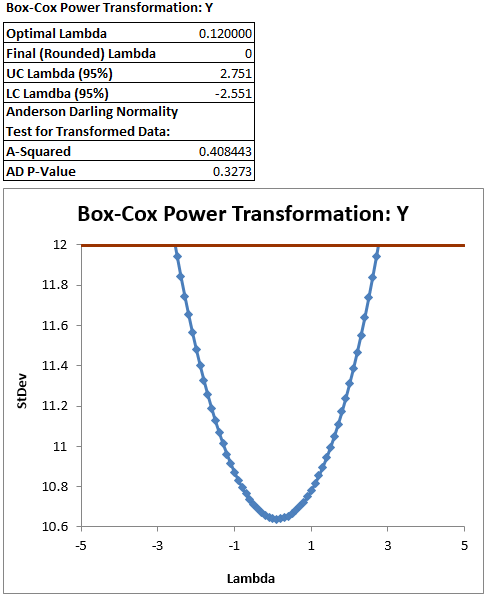
The software looks for the optimal value of lambda that minimizes the SSE (Sum of Squares of Error). In this case the minimum value is 0.12. The transformed Y can also be saved in another column. The transformed Y is also listed in Column G in the newly generated tab “Box-Cox (1)
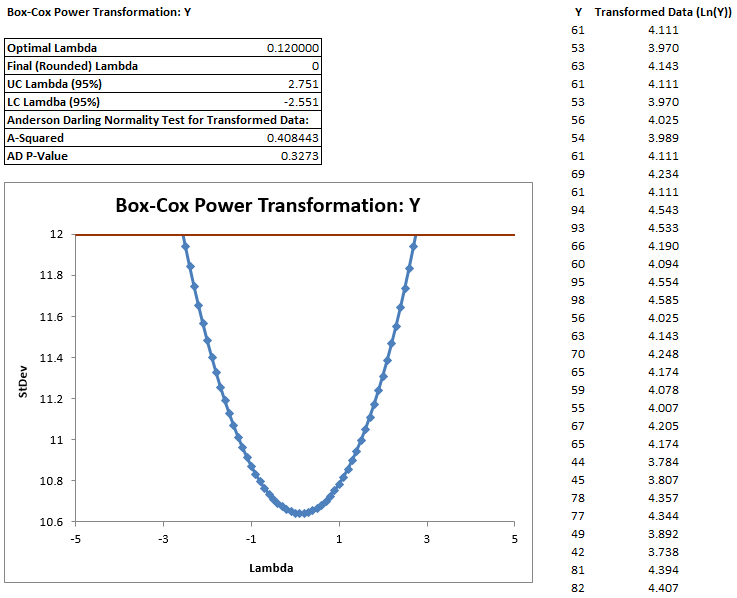Use the Anderson–Darling test to test the normality of the transformed data

• H₀: The data are normally distributed.
• H₁: The data are not normally distributed.

Model summary: If p-value > alpha level (0.05), we fail to reject the null. Otherwise, we reject the null. In this example, p-value = 0.327 > alpha level (0.05). The data are normally distributed.