Box Cox Transformation with JMP
What is a Box Cox Transformation?
Data transforms are usually applied so that the data appear to more closely meet assumptions of a statistical inference model to be applied or to improve the interpret-ability or appearance of graphs.
- Power transformation is a class of transformation functions that raise the response to some power. For example, a square root transformation converts X to X1/2
- Box-Cox transformation is a popular power transformation method developed by George E. P. Box and David Cox
Box Cox Transformation Formula
The formula of the Box Cox transformation is:
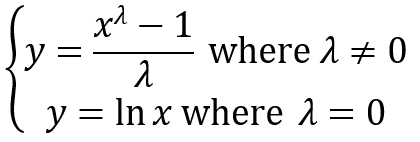
Where:
- y is the transformation result
- x is the variable under transformation
- λ is the transformation parameter.
How to Use JMP to Perform a Box Cox Transformation
JMP provides the best Box-Cox transformation with an optimal λ that minimizes the model SSE (sum of squared error). Here is an example of how we transform the non-normally distributed response to normal data using Box-Cox method.
Data File: “Box-Cox.jmp”
Run Box Cox Transformation in JMP:
Step 1: Test the normality of the original data set.
- Click Analyze -> Distribution
- Select Y as “Y, Column”
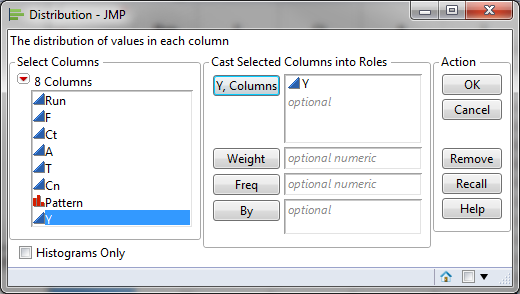
- Click “OK”
- Click on the red triangle button next to “Y”
- Select Continuous Fit -> Normal
- Click on the red triangle button next to “Fitted Normal”
- Select “Goodness of Fit”
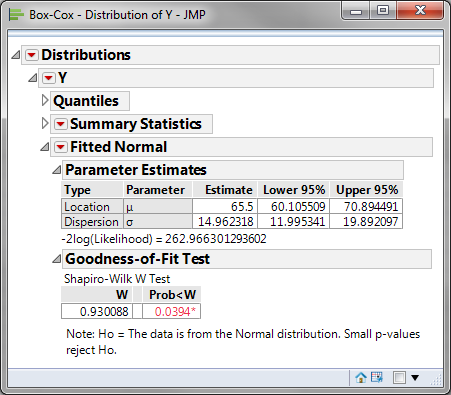
Normality Test:
- H0: The data are normally distributed
- H1: The data are not normally distributed
If p-value > alpha level (0.05), we fail to reject the null hypothesis. Otherwise, we reject the null. In this example, p-value = 0.0394 < alpha level (0.05). The data are not normally distributed.
Step 2: Run the Box-Cox Transformation:
- Click Analyze -> Fit Model
- Select Y as “Y”
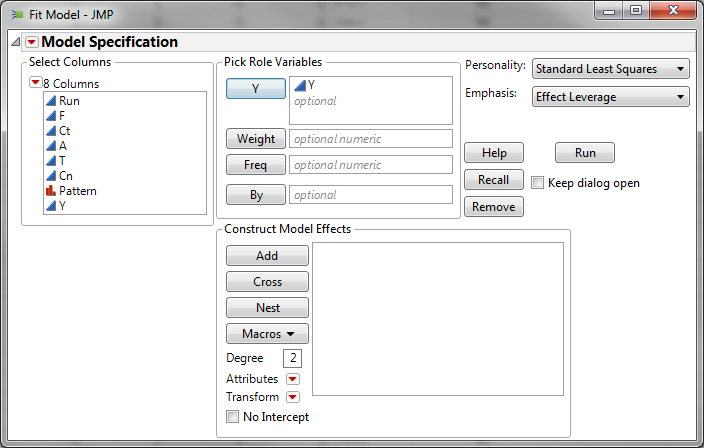
- Click “OK”
- Click on the red triangle button next to “Response Y”
- Select Factor Profiling -> Box Cox Y Transformation
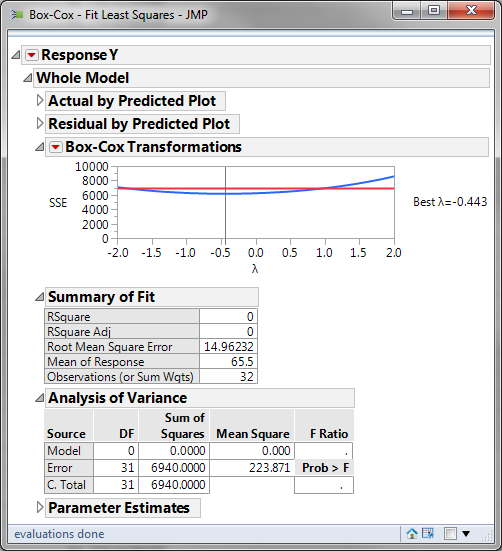
- A chart of sum of squared error (SSE) and λ is plotted at the bottom of the analysis output.
- Click on the red triangle button next to “Box-Cox Transformations”
- Select “Save Best Transformation”
- A new column called “Y X” will be added to the data table.
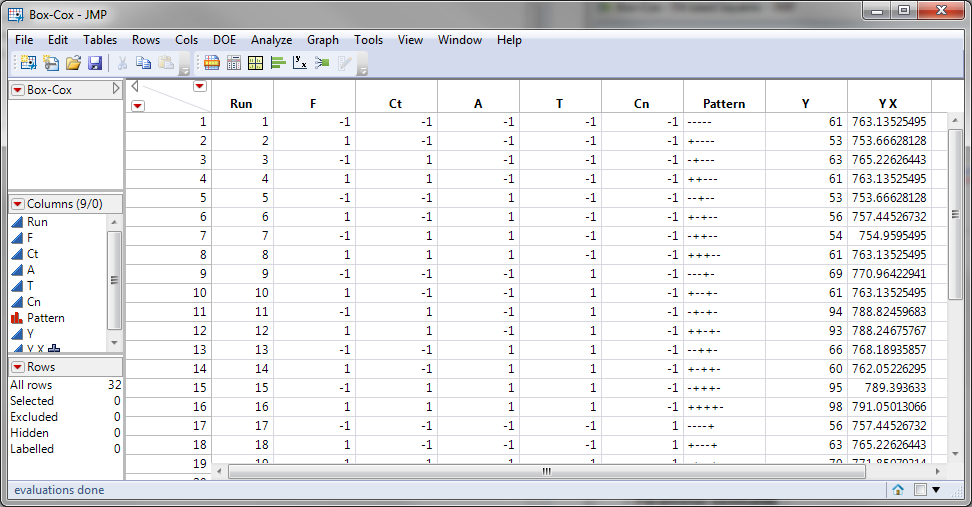
The software looks for the optimal value of lambda that minimizes the SSE (Sum of Squares of Error). In this case the minimum value is 0.12. The transformed Y can also be saved in another column.
The Box-Cox Transformations chart presents how the sum of squared errors change across λ ranging from -2 to 2. Based on the chart, when λ is between -0.5 and 0.0, the transformation is the best with minimum SSE.
Step 3: Test the normality of the newly transformed data set.
- Click Analyze -> Distribution
- Select “Y X” as “Y, Column”
- Click “OK”
- Click on the red triangle button next to “Y X”
- Select Continuous Fit -> Normal
- Click on the red triangle button next to “Fitted Normal”
- Select “Goodness of Fit”
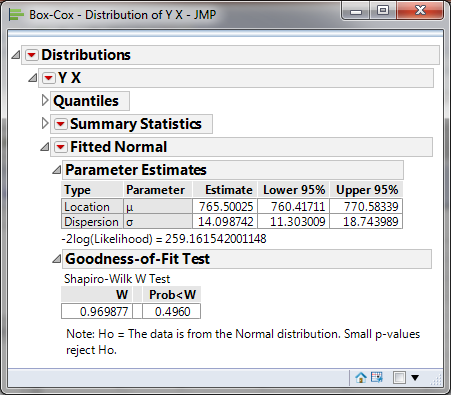
- H0: The data are normally distributed
- H1: The data are not normally distributed
Model summary: If p-value > alpha level (0.05), we fail to reject the null. Otherwise, we reject the null. In this example, p-value = 0.4897 > alpha level (0.05). The data are normally distributed.

