Fractional Factorial Designs with Minitab

What Are Fractional Factorial Experiments?

In simple terms, a fractional factorial experiment is a subset of a full factorial experiment.

• Fractional factorials use fewer treatment combinations and runs.
• Fractional factorials are less able to determine effects because of fewer degrees of freedom available to evaluate higher order interactions.
• Fractional factorials can be used to screen a larger number of factors.
• Fractional factorials can also be used for optimization.

Why Fractional Factorial Experiments?

To run a full factorial experiment for k factors, we need 2^k unique treatments. In other words, we need resources that can afford at least 2^k runs.

With k increasing, the number of runs required in full factorial experiments rises dramatically even without any replications, and the percentage of degrees of freedom spent on the main effects decreases. However, the higher order interactions (3 or 4 factor interactions) can typically be ignored, which allows us to run fewer trials to understand the main effects and two-way interactions.

The main effects and two-way interaction are the key effects we need to evaluate. The higher order the interaction is, the more we can ignore it.

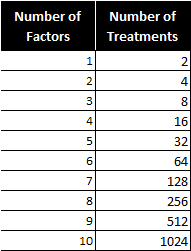
Notice the number of treatments increases dramatically as factors are added.

How Does a Fractional Factorial Work?

We are trying to find the cause-and-effect relationship between a response (Y) and three factors (factor A, B, and C) and their interactions (AB, BC, AC, and ABC). As follows is the 2³ full factorial design (2 level 3 factor). There are eight treatment combinations (2 * 2 * 2).

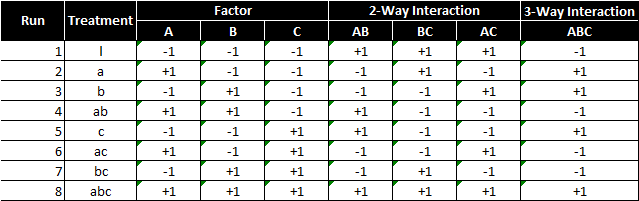
To perform a 2³ full factorial experiment, we need to run at least eight unique treatments (2 * 2 * 2).
What if we only have enough resources to run four treatments?
As a result, we need to carefully select a subset from the eight treatments so that all of our main effects can be evaluated and the design can be kept balanced and orthogonal.

Example of an invalid design

This design is invalid because only the low setting of factor C is tested. We cannot evaluate the main effect of factor C using this design. Remember orthogonality?

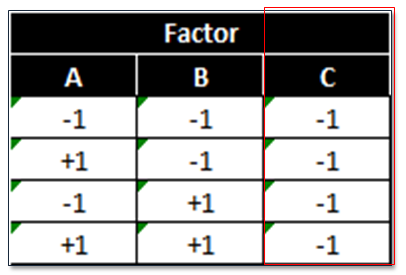
This design is also invalid because it is neither balanced nor orthogonal. Checking orthogonality: the sum of AC interaction signs should equal zero (0).

• Run 1 (−)
• Run 2 (−)
• Run 3 (−)
• Run 4 (+)
• Sum (−1)

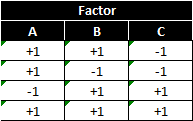
This design has a low and high setting for each factor, but is not orthogonal. To select the four treatments run in the 2³⁻¹ fractional factorial experiment, we start from the 2² full factorial design of experiment. If we replace the two-way interaction (AB) column with the factor C column, the design will be valid.

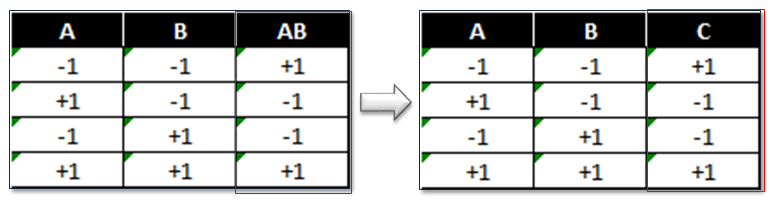Imagine a two-factor full factorial with factors A and B. We also learn about the interaction of A and B. In a fractional factorial, we sacrifice learning about the two-way interaction between A and B, and substitute factor C.

2³⁻¹ Fractional Factorial Design Pattern

This pattern implies three factors and four treatments.

Note: We also call this kind of design a half-factorial design since we only have half of the treatments that we would have in a full factorial design. In 2³⁻¹ fractional factorial design of experiment, the effect of three-way interaction (ABC) is not measurable since it only has “+1”.
In four runs, we are able to run high and low settings for each of the three factors. The three-way interaction ABC is only at the high setting. In the 2³⁻¹ fractional factorial design, we notice that the column of each main effect has identical “+1” and “−1” values with one two-way interaction column.

• A and BC
• B and AC
• C and AB

In this situation, we say that A is aliased with BC or A is the alias of BC. By multiplying any column with itself, we obtain the identity (I).

A*A=I

The product of any column and the identity is the column itself.

A*I=A

Column ABC is called the generator. By multiplying any column with the generator, we obtain its alias.

A*ABC=(A*A)*BC=I*BC=BC

Use Minitab to Run a Fractional Factorial Experiment

Step 1: Initiate the experiment design

1. Click Stat → DOE → Factorial → Create Factorial Design.
2. A new window named “Create Factorial Design” pops up.
3. Select the radio button “2-level factorial (default generators).”
4. Enter “3” as the “Number of factors.”
   
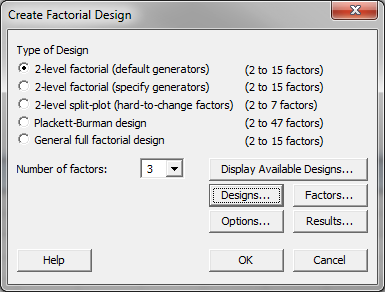
5. Click on the “Design” button in the window “Create Factorial Design” and another new window named “Create Factorial Design – Designs” pops up.
6. Highlight the “1/2 fraction” design in the box.
7. Select “2” as the “Number of replicates for corner points.”
   
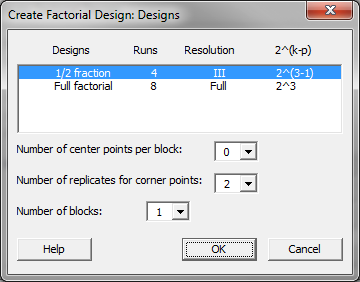
8. Click “OK” in the window “Create Factorial Design – Designs.”
9. Click “OK” in the window “Create Factorial Design.”
10. The design table is created in the data table.
    

This is what the design table should look like.

Step 1.2 (optional): Define the names and the two levels for individual factors

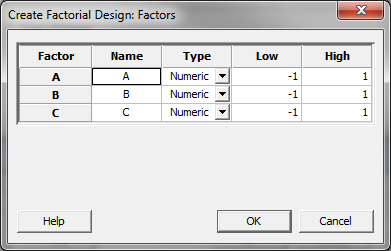
1. Click on the “Factors” button in the window “Create Factorial Design” and a new window named “Create Factorial Design – Factors” appears.
2. Enter the names and the levels for individual factors. In this example, we keep the default names and levels for factors A, B, and C.
   

Step 2: Implement the experiment and record the results in the DOE table

Step 3: Fit the model using the experiment results

1. Click Stat → DOE → Factorial → Analyze Factorial Design.
2. A new window named “Analyze Factorial Design” appears.
3. Select “Y” as the “Responses.”
   
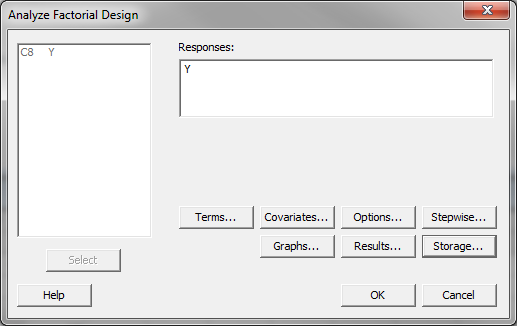
4. Click on the “Storage” button and another new window named “Analyze Factorial Design – Storage” pops up.
5. Check the box “Fits” and “Residuals” so that both fitted responses and the residuals would be saved in the data table.
   
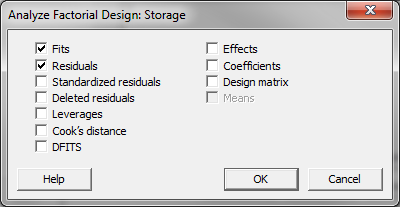
6. Click “OK” in the window “Analyze Factorial Design – Storage.”
7. Click “OK” in the window “Analyze Factorial Design.”
8. The DOE analysis results appear in the session window.

Step 4: Analyze the model results

1. Check whether the model is statistically significant.
2. Check which factors are insignificant.

If any independent variables are not significant, remove them one at a time and rerun the model until all the independent variables in the model are significant.

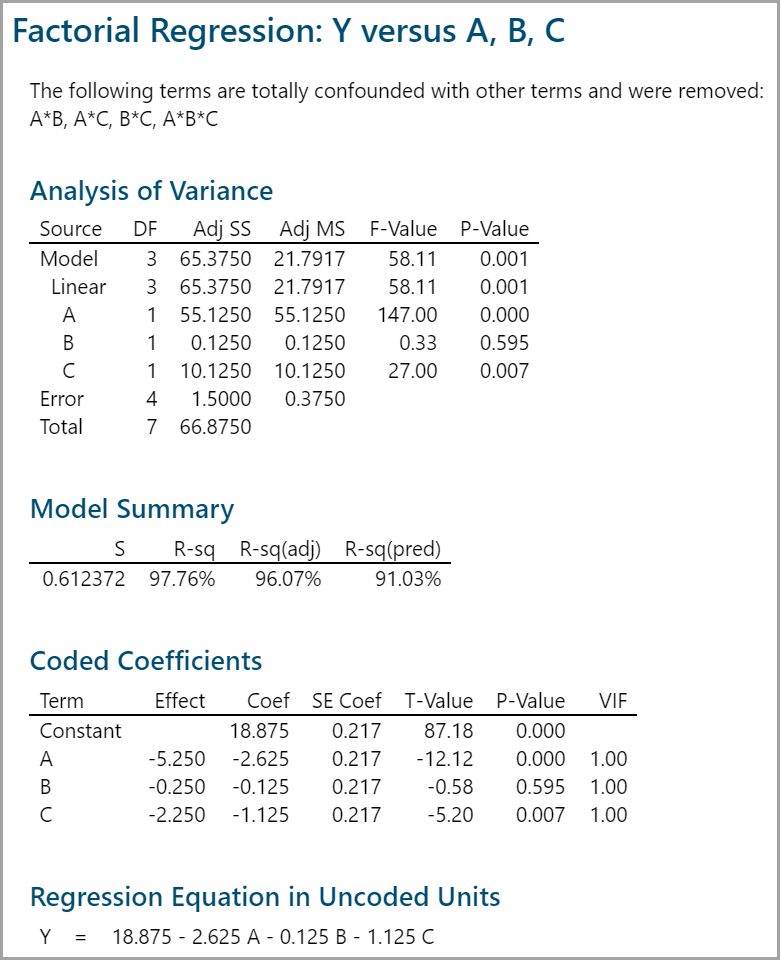The p-value of factor B is greater than the alpha level (0.05), so it is not statistically significant. In this example, since factor B is not statistically significant, it needs to be removed from the model.

Step 5.0:

1. Click Stat → DOE → Factorial → Analyze Factorial Design.
2. A new window named “Analyze Factorial Design” appears.
3. Select “Y” as the “Responses.”
   
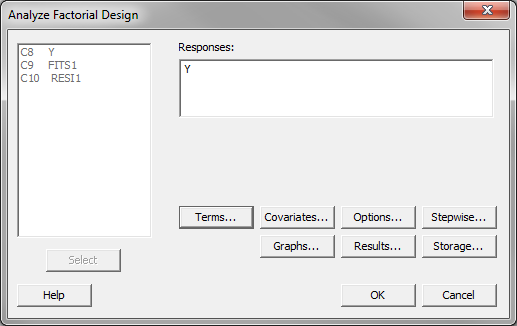
4. Click on the “Terms” button and another new window named “Analyze Factorial Design – Terms” pops up.
5. Deselect the factor “B:B” from the box “Selected Terms.”
   
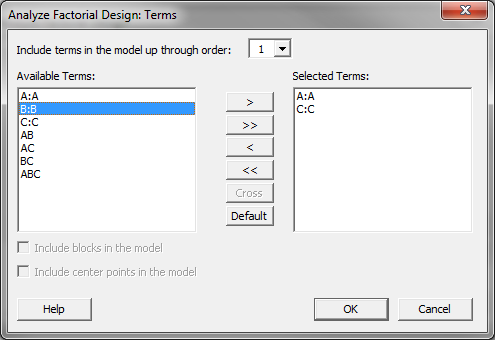
6. Click “OK” in the window “Analyze Factorial Design – Terms.”
7. Click “OK” in the window “Analyze Factorial Design.”
8. The DOE analysis results appear in the session window.

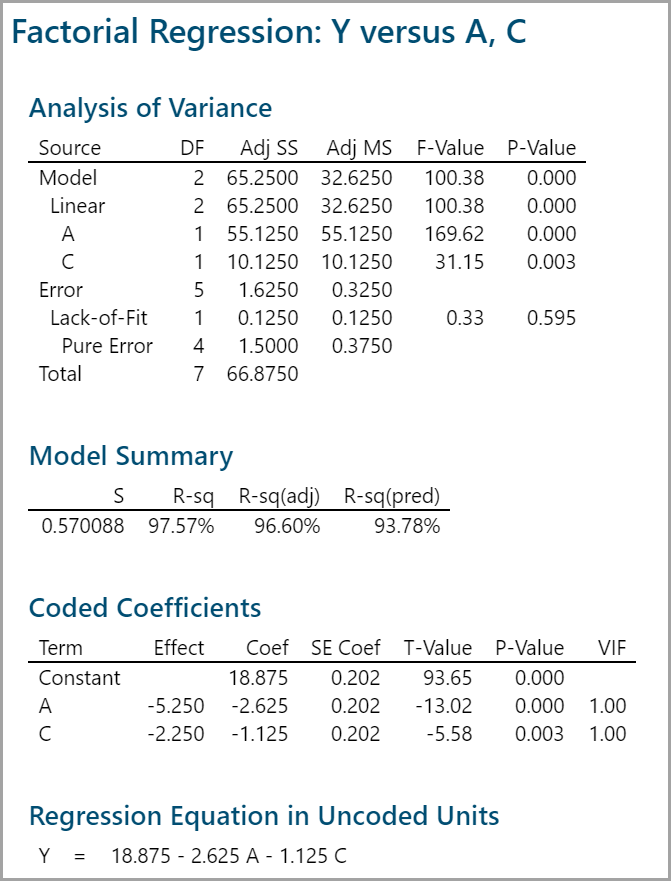
The p-values of all the independent variables are smaller than 0.05. There is no need to remove any independent variables from the model.

Step 5.1: Check whether residuals are normally distributed with mean equal to zero.

1. Click Stat → Basic Statistics → Graphical Summary.
2. A new window named “Graphical Summary” appears.
3. Select “RESI2” as the “Variables.”
   
4. Click “OK.”
5. The histogram and the normality test of the residuals appear in the newly-generated window.
   

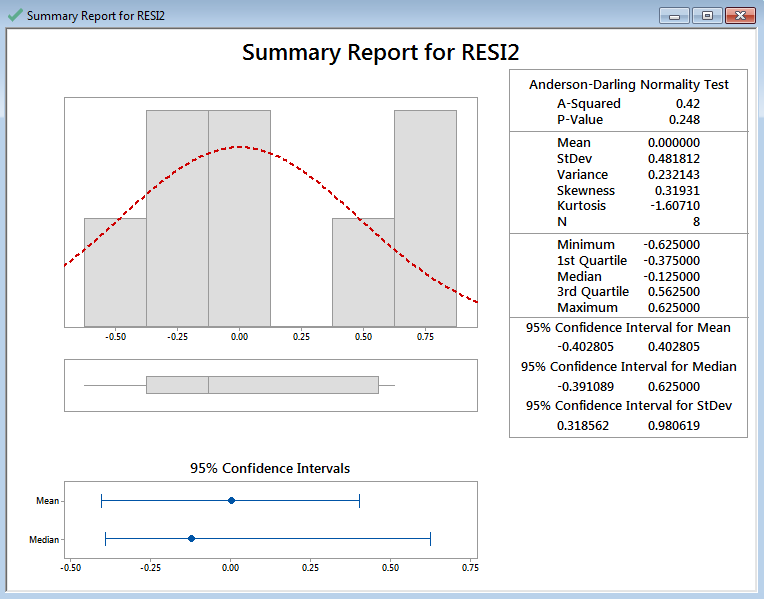
If the p-value of the normality test is greater than the alpha level (0.05), the residuals are normally distributed. The p-value of the normality test is larger than alpha level (0.05). The residuals are normally distributed. Residuals’ mean is zero.

Step 5.2: Check whether the residuals are independent.

1. Click Stat → Control Charts → Variables Charts for Individuals → I-MR.
2. A new window named “Individuals – Moving RangeChart” appears.
3. Select the “RESI2” as the “Variables.”
   
4. Click “OK.”
5. The control charts appear in the newly-generated window.
   

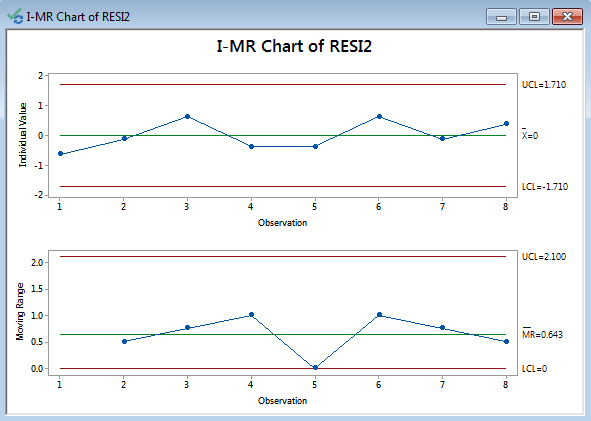
If no data points on the control charts fail any tests, the residuals are in control and independent of each other.

Note: The prerequisite of plotting I-MR chart for residuals: the residuals are in the time order. These are the control charts for estimating whether residuals are independent.

Step 5.3: Check whether the residuals have equal variance across the predicted responses.

1. Click Graph → Scatterplot.
2. A new window named “Scatterplots” pops up.
3. Click “OK” in the window “Scatterplots.”
4. Another window named “Scatterplot Simple” pops up.
5. Select “RESI2” as “Y variables” and “FITS2” as “X variables.”
   
6. Click “OK” in the window “Scatterplot– Simple.”
7. The scatterplot between the fitted responses and the residuals appears in a new window.
   

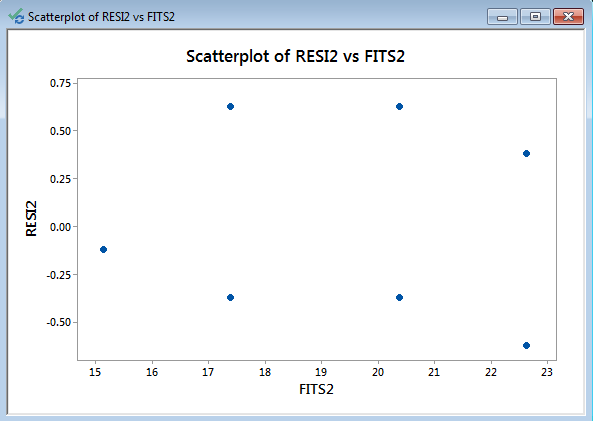
Model summary: We look for patterns in which the residuals tend to have even variation across the entire range of the fitted response values.