Mann Whitney Test with SigmaXL
What is the Mann Whitney Test with SigmaXL?
The Mann Whitney test with SigmaXL is a statistical test (also called Mann–Whitney U test or Wilcoxon rank-sum test) is a statistical hypothesis test to compare the medians of two populations that are not normally distributed. In a non-normal distribution, the median is the better representation of the center of the distribution.
- Null Hypothesis (H0): η1 = η2
- Alternative Hypothesis (Ha): η1 ≠ η2
Where:
- η1 is the median of one population
- η2 is the median of the other population
- The null hypothesis is that the medians are equal, and the alternative is that they are not equal
Mann Whitney Test Assumptions
- The sample data drawn from the populations of interest are unbiased and representative.
- The data of both populations are continuous or ordinal when the spacing between adjacent values is not constant. (Reminder: Ordinal data—A set of data is said to be ordinal if the values can be ranked or have a rating scale attached. You can count and order, but not measure, ordinal data.)
- The two populations are independent to each other.
- The Mann–Whitney test is robust for the non-normally distributed population.
- The Mann–Whitney test can be used when shapes of the two populations’ distributions are different.
How Mann Whitney Test Works
Step 1:
Group the two samples from two populations (sample 1 is from population 1 and sample 2 is from population 2) into a single data set and then sort the data in ascending order ranked from 1 to n, where n is the total number of observations.
Step 2:
Add up the ranks for all the observations from sample 1 and call it R1. Add up the ranks for all the observations from sample 2 and call it R2.
Step 3:
Calculate the test statistics
![]()
Where:
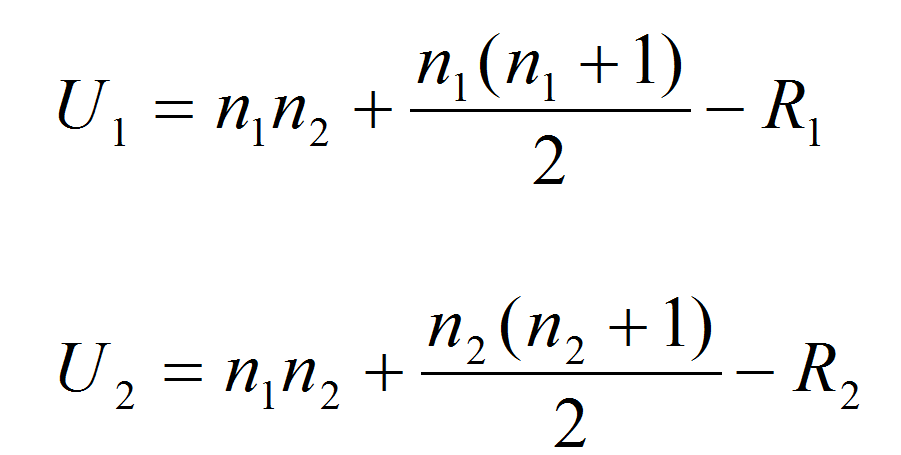
and where:
- n1 and n2 are the sample sizes
- R1 and R2 are the sum of ranks for observations from sample 1 and 2 respectively
Step 4:
Make a decision on whether to reject the null hypothesis.
- Null Hypothesis (H0): η1 = η2
- Alternative Hypothesis (Ha): η1 ≠ η2
If both of the sample sizes are smaller than 10, the distribution of U under the null hypothesis is tabulated.
- The test statistic is U and, by using the Mann–Whitney table, we would find the p-value.
- If the p-value is smaller than alpha level (0.05), we reject the null hypothesis.
- If the p-value is greater than alpha level (0.05), we fail to reject the null hypothesis.
- If both sample sizes are greater than 10, the distribution of U can be approximated by a normal distribution. In other words, (U-μ)/σ follows a standard normal distribution.
Z_calc=(U-μ)/σ
Where:
μ=(n_1 n_2)/2
σ=√(√(n_1 n_2 (n_1+n_2+1))/12)
If the sample sizes are greater than 10, then the distribution of U can be approximated by a normal distribution. The U value is then plugged into the formula seen here to calculate a Z statistic.
When |Zcalc| is greater than Z value at α/2 level (e.g. when α = 5%, the z value we compare |Zcalc| to is 1.96), we reject the null hypothesis.
Run a Mann Whitney Test with SigmaXL
Case study: We are interested in comparing customer satisfaction between two types of customers using a nonparametric (i.e. distribution-free) hypothesis test: Mann–Whitney test.
Data File: “Mann–Whitney” tab in “Sample Data.xlsx”
- Null Hypothesis (H0): η1 = η2
- Alternative Hypothesis (Ha): η1 ≠ η2
Steps to run a Mann–Whitney Test in SigmaXL:
- Select the entire range of data (both “Customer Type” and “Overall Satisfaction”)
- Click SigmaXL -> Statistical Tools -> Nonparametric Tests -> 2 Sample Mann-Whitney
- A new window named “2 Sample Mann Whitney” pops up with the selected range populated in the box under “Please select your data”
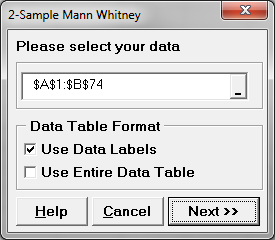
- Click “Next>>”
- A new window named “2 Sample Mann-Whitney” appears
- Select “Overall Satisfaction” as the “Numeric Data Variables (Y)”
Select “Customer Type” as the “Group Category (X)”
Select “Not Equal To” as the “Ha”
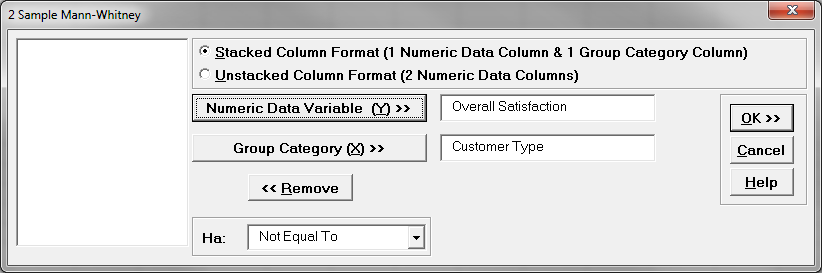
- Click “OK>>”
- The Mann-Whitney test results appear in the newly generated tab “2 Sample Mann-Whitney (1)”
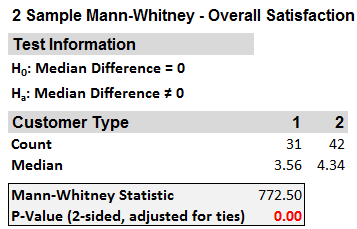
Model summary: The p-value of the test is lower than alpha level (0.05); so we reject the null hypothesis and conclude that there is a statistically significant difference between the overall satisfaction medians of the two customer types.
The result of the test is boxed in: The p-value is lower than the alpha value of 0.05; therefore, we must reject the null hypothesis and claim that there is a significant difference between the median customer satisfaction levels of the two groups.
Join Our Community
Instant access to hundreds of "How to" articles, Tools, Templates, Roadmaps, Data-Files.. Everything Lean Six Sigma! Come on in! Welcome to our community of Lean Six Sigma certified professionals.


