Multiple Linear Regression with Minitab
What is Multiple Linear Regression with Minitab?
The multiple linear regression with Minitab is a statistical technique to model the relationship between one dependent variable and two or more independent variables by fitting the data set into a linear equation.
The difference between simple linear regression and multiple linear regression:
- Simple linear regression only has one predictor.
- Multiple linear regression has two or more predictors.
Use Minitab to Run a Multiple Linear Regression
Case study: We want to see whether the scores in exams one, two, and three have any statistically significant relationship with the score in the final exam. If so, how are they related to the final exam score? Can we use the scores in exams one, two, and three to predict the score in the final exam?
Data File: "Multiple Linear Regression.MTW found within the zip file: MTB_Data_Files.zip
Step 1: Determine the dependent and independent variables, all should be continuous. Y (dependent variable) is the score of the final exam. X1, X2, and X3 (independent variables) are the scores of exams one, two, and three respectively. All x variables are continuous.
Step 2: Start building the multiple linear regression model
- Click Stat → Regression → Regression → Fit Regression Model
- A new window named “Regression” pops up.
- Select “FINAL” as “Response” and “EXAM1”, “EXAM2” and “EXAM3” as “Predictors.”

- Click the “Graph” button, select the radio button “Four in one” and click “OK.”

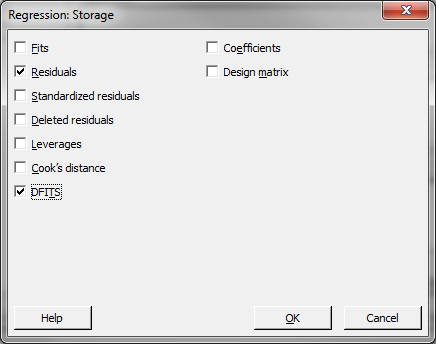
- Click the “Storage” button, check the boxes of “Residuals” and “DFITS” and click “OK.”
- Click “OK” in the window named “Regression.”
- The regression analysis results appear in a session window, and the four residual plots appear in another window named “Residual Plots for FINAL.”
Step 3: Check whether the whole model is statistically significant. If not, we need to re-examine the predictors or look for new predictors before continuing.
- H0: The model is not statistically significant (i.e., all the parameters of predictors are not significantly different from zeros).
- H1: The model is statistically significant (i.e., at least one predictor parameter is significantly different from zero).
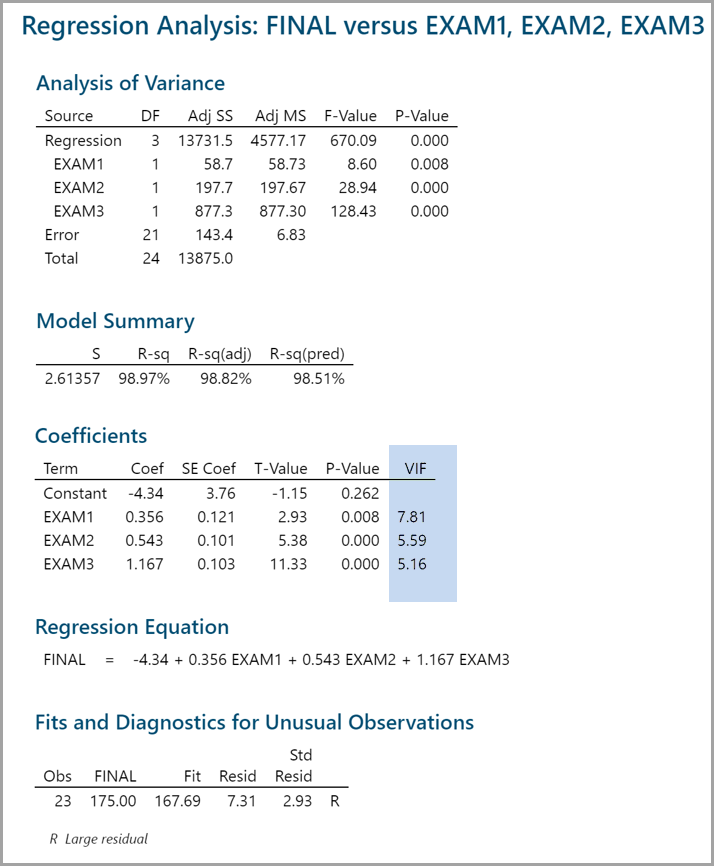
In this example, the p-value is much smaller than the alpha level (0.05). Hence we reject the null hypothesis; the model is statistically significant.
Step 4: Check whether multicollinearity exists in the model.
The VIF information is automatically generated in the table of Coefficients.
 We use the VIF (Variance Inflation Factor) to determine if multicollinearity exists.
We use the VIF (Variance Inflation Factor) to determine if multicollinearity exists.
Multicollinearity
Multicollinearity is the situation when two or more independent variables in a multiple regression model are correlated with each other. Although multicollinearity does not necessarily reduce the predictability for the model as a whole, it may mislead the calculation for individual independent variables. To detect multicollinearity, we use VIF (Variance Inflation Factor) to quantify its severity in the model.
Variance Inflation Factor (1)
VIF quantifies the degree of multicollinearity for each individual independent variable in the model.
VIF calculation:
Assume we are building a multiple linear regression model using p predictors. Two steps are needed to calculate VIF for X1. Step 1: Build a multiple linear regression model for X1 by using X2, X3 . . . Xp as predictors. Step 2: Use the R2 generated by the linear model in step 1 to calculate the VIF for X1. Apply the same methods to obtain the VIFs for other X’s. The VIF value ranges from one to positive infinity.
Variance Inflation Factor (2)
Rules of thumb to analyze variance inflation factor (VIF):
- If VIF = 1, there is no multicollinearity.
- If 1 < VIF < 5, there is small multicollinearity.
- If VIF ≥ 5, there is medium multicollinearity.
- If VIF ≥ 10, there is large multicollinearity.
How to Deal with Multicollinearity
- Increase the sample size.
- Collect samples with a broader range for some predictors.
- Remove the variable with high multicollinearity and high p-value.
- Remove variables that are included more than once.
- Combine correlated variables to create a new one.
In this section, we will focus on removing variables with high VIF and high p-value.
Step 5: Deal with multicollinearity:
- Identify a list of independent variables with a VIF higher than 5. If no variable has VIF higher than 5, go to Step 6 directly.
- Among the variables identified in Step 5.1, remove the one with the highest p-value.
- Run the model again, check the VIFs, and repeat Step 5.1.
Note: we only remove one independent variable at a time.
In this example, all three predictors have VIFs higher than 5. Among them, EXAM1 has the highest p-value. We will remove EXAM1 from the equation and run the model again.
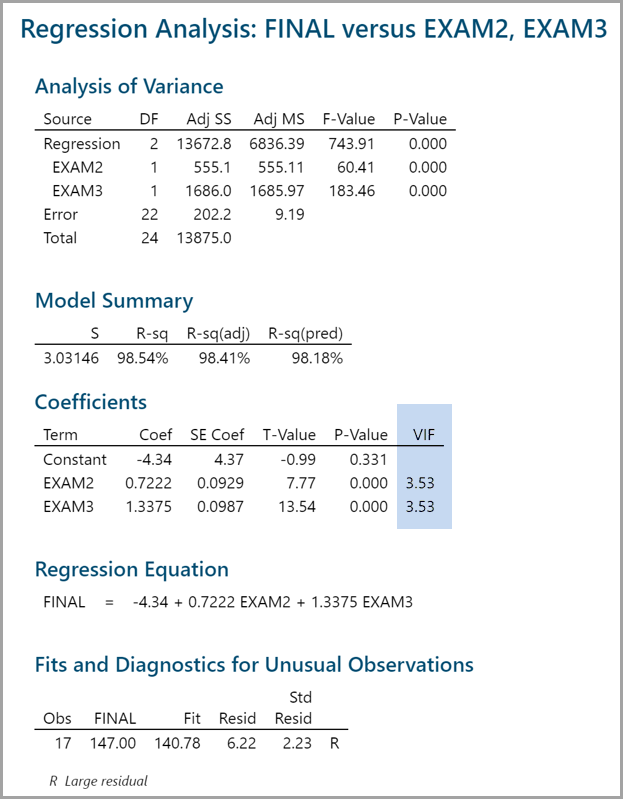
 Run the new multiple linear regression with only two predictors (i.e., EXAM2 and EXAM3).
Run the new multiple linear regression with only two predictors (i.e., EXAM2 and EXAM3).
Check the VIFs of EXAM2 AND EXAM3. They are both smaller than 5; hence, there is little multicollinearity existing in the model.
 Step 6: Identify the statistically insignificant predictors. Remove one insignificant predictor at a time and run the model again. Repeat this step until all the predictors in the model are statistically significant.
Step 6: Identify the statistically insignificant predictors. Remove one insignificant predictor at a time and run the model again. Repeat this step until all the predictors in the model are statistically significant.
Insignificant predictors are the ones with a p-value higher than the alpha level (0.05). When p > alpha level, we fail to reject the null hypothesis; the predictor is insignificant.
- H0: The predictor is not statistically significant.
- H1: The predictor is statistically significant.
As long as the p-value is greater than 0.05, remove the insignificant variables one at a time in the order of the highest p-value. Once one insignificant variable is eliminated from the model, we need to run the model again to obtain new p-values for other predictors left in the new model. In this example, both predictors’ p-values are smaller than the alpha level (0.05). As a result, we do not need to eliminate any variables from the model.
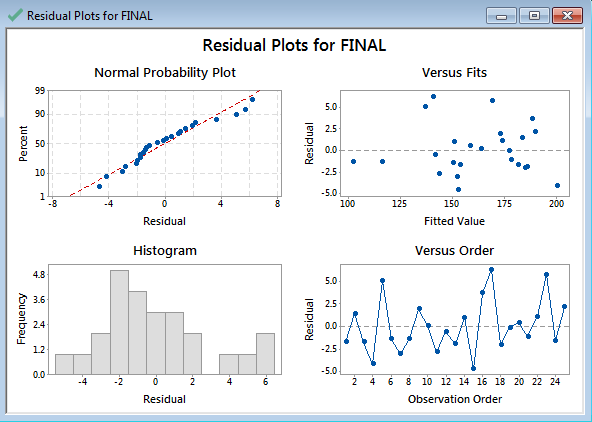 Step 7: Interpret the regression equation
Step 7: Interpret the regression equation
The multiple linear regression equation appears automatically at the top of the session window. “Parameter Estimates” section provides the estimates of parameters in the linear regression equation.
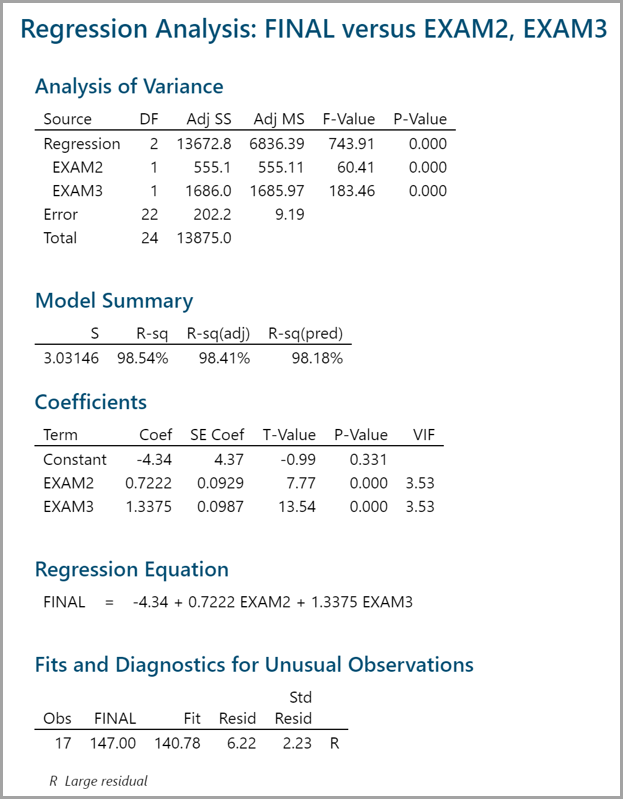 Now that we have removed multicollinearity and all the insignificant predictors, we have the parameters for the regression equation.
Now that we have removed multicollinearity and all the insignificant predictors, we have the parameters for the regression equation.
Interpreting the Results
Rsquare Adj = 98.4%
- 98% of the variation in FINAL can be explained by the predictor variables EXAM2 & EXAM3.
P-value of the F-test = 0.000
- We have a statistically significant model.
Variables p-value:
- Both are significant (less than 0.05).
VIF
- EXAM2 and EXAM3 are both below 5; we’re in good shape!
Equation: −4.34 + 0.722*EXAM2 + 1.34*EXAM3
- −4.34 is the Y intercept, all equations will start with −4.34.
- 722 is the EXAM2 coefficient; multiply it by EXAM2 score.
- 34 is the EXAM3 coefficient; multiply it by EXAM3 score.
Let us say you are the professor again, and this time you want to use your prediction equation to estimate what one of your students might get on their final exam.
Assume the following:
- Exam 2 results were: 84
- Exam 3 results were: 102
Use your equation: −4.34 + 0.722*EXAM2 + 1.34*EXAM3
Predict your student’s final exam score:
−4.34 + (0.722*84) + (1.34*102) =−4.34 + 60.648 + 136.68 = 192.988
Model summary: Nice work again! Now you can use your “magic” as the smart and efficient professor and allocate your time to other students because this one projects to perform much better than the average score of 162. Now that we know that exams two and three are statistically significant predictors, we can plug them into the regression equation to predict the results of the final exam for any student.
More Articles and Free Tools - Join Today
Learn more about using Minitab for Six Sigma and all the other amazing tools and techniques that can be used in your everyday work life to shine among your peers and perform at your highest potential. Enroll in our Lean Six Sigma Black Belt Online Training from Lean Sigma Corporation and continue learning to grow your career!


I cannot find the data set for this blog within Minitab 18. Please help. Thank you!
Hi Dan
The data file in .xlsx format is: https://www.leansigmacorporation.com/support-files/Sample_Data.xlsx
The zip file with .mtw files is: https://www.leansigmacorporation.com/support-files/MTB_Data_Files.zip
Let me know if you have any other questions
Very Nice informative article. Thanks denis
This is a superb article. Thank you.
Dear Denise Coleman
Thanks for your article.
But I have got a question regarding to perform multiple regression in nonlinear mode for example if our data can not simply fit by multiple linear regression. Is it anyway to perform this test by Minitab or other statistical softwares?
Sorry to trouble you, but can I ask you for a favor? In step 3, we need to check the p-value, but in the Analysis of Variance Table, we have 4 values in the “p-value” column (0.000, 0.008, 0.000, 0.000). I don’t know if I need to compare all of them with 0.05 or I just compare the first value (in the first row which named regression) with 0.05?