Simple Linear Regression with Minitab

What is Simple Linear Regression with Minitab?

The Simple linear regression with Minitab is a statistical technique to fit a straight line through the data points. It models the quantitative relationship between two variables. It is simple because only one predictor variable is involved. It describes how one variable changes according to the change of another variable. Both variables need to be continuous; there are other types of regression to model discrete data.

Run a Simple Linear Regression with Minitab

Case study: We want to see whether the score on exam one has any statistically significant relationship with the score on the final exam. If yes, how much impact does exam one have on the final exam?
Data File: “Simple Linear Regression” tab in “Sample Data.xlsx”

Step 1: Determine the dependent and independent variables. Both should be continuous variables.

• Y (dependent variable) is the score of final exam.
• X (independent variable) is the score of exam one.

Step 2: Create a scatter plot to visualize whether there seems to be a linear relationship between X and Y.

1. Click Graph → Scatterplot.
2. A new window named “Scatterplots” pops up.
3. Click “OK.”
4. A new window named “Scatterplot– Simple” pops up.
5. Select “FINAL” as “Y variables” and “EXAM1” as “X variables.”
   
6. Click “OK.”
7. A scatter plot is generated in a new window.
   

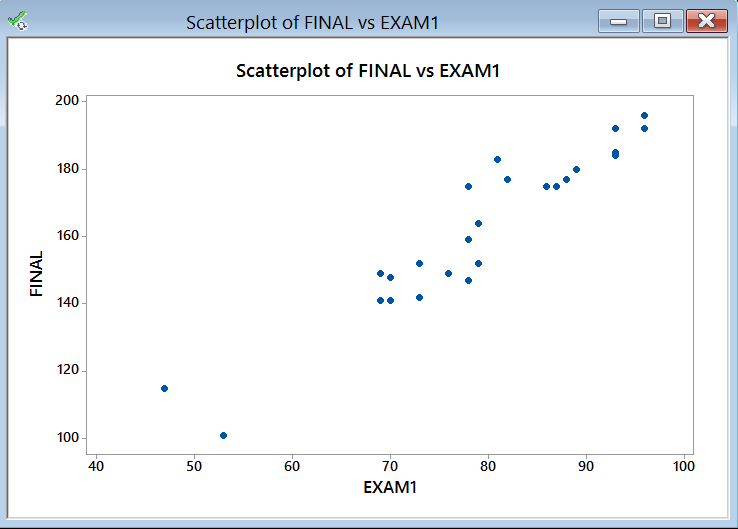
Based on the scatter plot, the relationship between exam one and final seems linear. The higher the score on exam one, the higher the score on the final. It appears you could “fit” a line through these data points.

Step 3: Run the simple linear regression analysis.

1. Click Stat → Regression → Regression → Fit Regression Model.
2. A new window named “Regression” pops up.
3. Select “FINAL” as “Response” and “EXAM1” as “Continuous Predictors.”
   
4. Click the “Storage” button.
5. Check the box of “Residuals” so that the residuals can be saved automatically in the last column of the data table.
   
6. Click “OK.”
7. The regression analysis results appear in the new window.
   

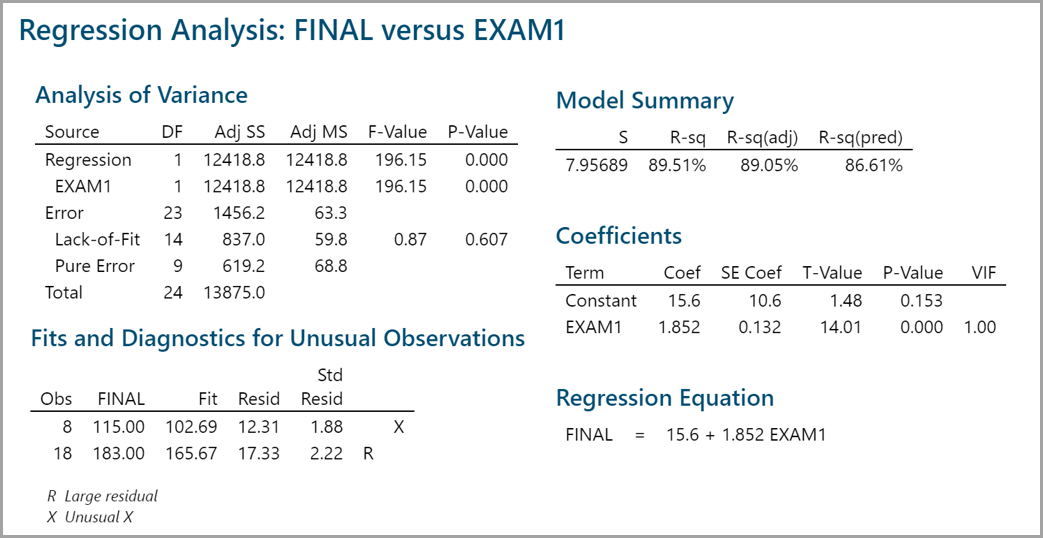
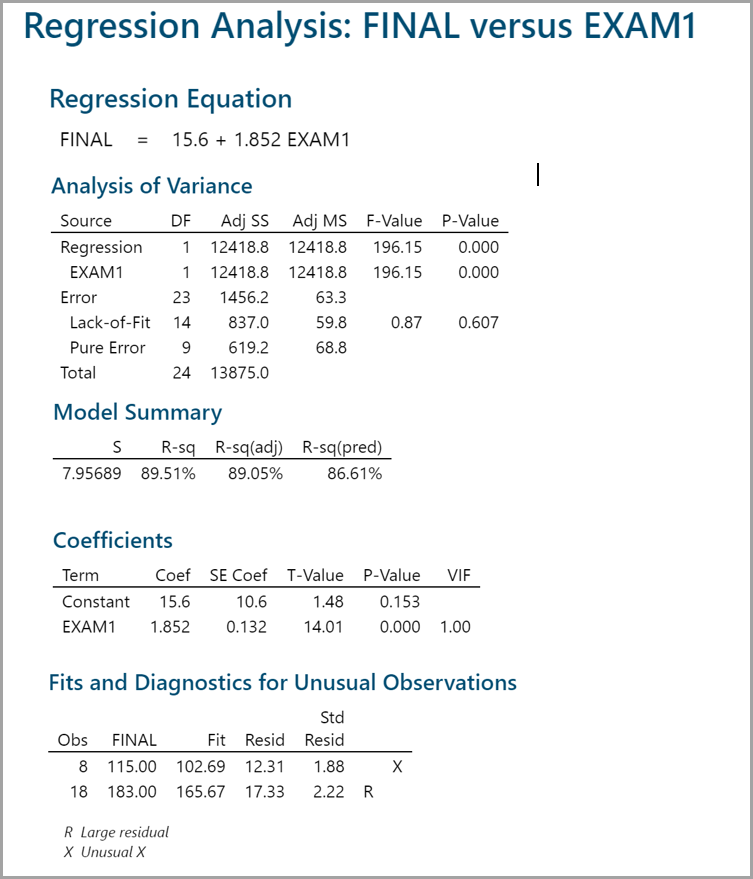
Step 4: Check whether the simple linear regression model is statistically significant. If not significant, we will need to re-examine the predictor or look for new predictors before continuing. R² measures the percentage of variation in the data set that can be explained by the model. 89.5% of the variability in the data can be accounted for by this linear regression model. “Analysis of Variance” section provides an ANOVA table covering degrees of freedom, sum of squares, and mean square information for total, regression and error. The p-value of the F-test is lower than the α level (0.05), indicating that the model is statistically significant.

The p-value is 0.0001; therefore, we reject the null and claim the model is statistically significant. The R square value says that 89.5% of the variability can be explained by this model.

Step 5: Understand regression equation

The estimates of slope and intercept are shown in “Parameter Estimate” section. In this example, Y = 15.6 + 1.85 × X, where X is the score on Exam 1 and Y is the final exam score. One unit increase in the score of Exam1 would increase the final score by 1.85.

Interpreting the Simple Linear Regression Results

Let us say you are the professor and you want to use this prediction equation to estimate what two of your students might get on their final exam.

Rsquare Adj = 89.0%

• 89% of the variation in FINAL can be explained by EXAM1

P-value of the F-test = 0.000

• We have a statistically significant model

Prediction Equation: 15.6 + 1.85 × EXAM1

• 6 is the Y intercept, all equations will start with 15.6
• 85 is the EXAM1 Coefficient: multiply it by EXAM1 score

Because the model is significant, and it explains 89% of the variability, we can use the model to predict final exam scores based on the results of Exam1.

Let us assume the following:

• Student “A” exam 1 results were: 79
• Student “B” exam 1 results were: 94

Remember our prediction equation 15.6 + 1.85 × Exam1?

Now apply the equation to each student:

Student “A” Estimate: 15.6 + (1.85 × 79) = 161.8

Student “B” Estimate: 15.6 + (1.85 × 94) = 189.5

Model summary: By simply replacing exam 1 scores into the equation we can predict their final exam scores. But the key thing about the model is whether or not it is useful. In this case, the professor can use the results to Figure out where to spend his time helping students.