One Sample Wilcoxon Test with JMP

What is the One Sample Wilcoxon Test?

The one sample Wilcoxon test is a hypothesis test to compare the median of one population with a specified value.

• Null Hypothesis (H₀): η = η₀
• Alternative Hypothesis (H_a): η ≠ η₀

It is an alternative test of one sample t-test when the data distribution is non-normal. It is more powerful than one sample sign test, but it assumes the data distribution is symmetric.

One Sample Wilcoxon Test Assumptions

• The sample data drawn from the population of interest are unbiased and representative
• The data are continuous or ordinal when the spacing between adjacent values is not constant
• The distribution of the data is symmetric about a median
• The one sample Wilcoxon test is robust for the non-normally distributed population

The assumptions are similar to other non-parametric tests, again the difference in the symmetry of the distribution.

How the One Sample Wilcoxon Test Works

Step 1: Create the following columns one by one:

• Column 1: All the raw observations (X)
• Column 2: The differences between each observation value and the hypothesized median (X – η₀)
• Column 3: The signs (+ or –) of column 2
• Column 4: The absolute value of column 2
• Column 5: The ranks of each item in column 4 in ascending order
• Column 6: The product of column 3 and column 5

Step 2: Calculate the test statistic W_calc , which is the sum of all the non-negative values in column 6.

Step 3: Decide on whether to reject the null hypothesis. Use the table of critical values for the Wilcoxon test to get the W_crit with a predetermined alpha level and number of observations.

If the W_calc is smaller than the W_crit, we fail to reject the null hypothesis and claim that there is no significant difference between the population median and the hypothesized median. To calculate the W statistic, sum all of the non-negative values in column 6. The W statistic is compared against the critical W value to assess the hypothesis.

Use JMP to Run a One Sample Wilcoxon Test

Case study: We are interested in comparing the overall satisfaction of customer type 1 against a specified benchmark satisfaction (3.5) using a nonparametric (i.e. distribution-free) hypothesis test: one sample Wilcoxon test.
Data File:“OneSampleWilcoxon.jmp”

• Null Hypothesis(H₀): η₁ = 3.5
• Alternative Hypothesis(H_a): η₁ ≠ 3.5

Steps to run a one sample Wilcoxon test in JMP:

1. Click Analyze -> Distribution
2. Select “Overall Satisfaction” as “Y, Columns”
   
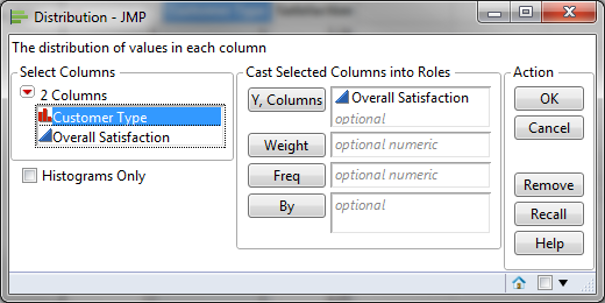
3. Click OK
4. Click on the red triangle button next to “Overall Satisfaction”
5. Click “Test Mean”
6. In the new pop-up window, enter the specified median (3.5) and check the box “Wilcoxon Signed Rank”
   
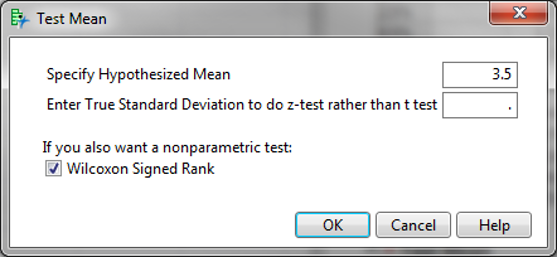
7. Click OK
   

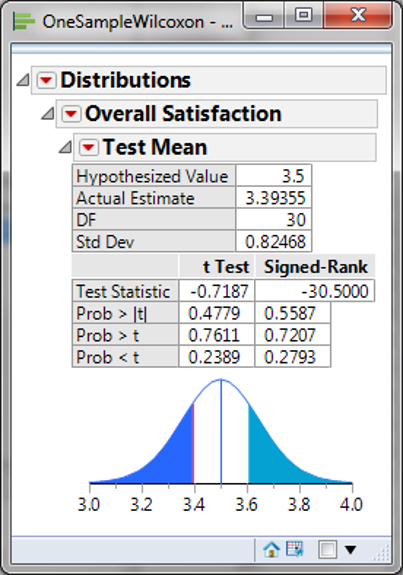
Model summary: The p-value of the one sample Wilcoxon test is 0.5587, higher than the alpha level (0.05), and we fail to reject the null hypothesis. There is no statistically significant difference between the overall satisfaction of customer type 1 and the benchmark satisfaction level. In this example, the software returns a p-value of 0.5587, much higher than the alpha value of 0.05. We fail to reject the null and claim that the population median is not statistically different than the specified value of 3.5.